Khái niệm phương sai
Phương sai (tiếng Anh là Variance), kí hiệu là σ2 trong thống kê. Trong đầu tư tài chính, phương sai lợi nhuận của các tài sản trong một danh mục đầu tư được sử dụng như một phương tiện để phân bổ tài sản một cách tốt nhất. Phương trình phương sai, trong đầu tư tài chính là công thức để so sánh hiệu quả của các thành phần trong danh mục đầu tư với nhau và so với giá trị hiệu quả trung bình.
Độ lệch chuẩn
Độ lệch chuẩn là giá trị chênh lệch trong tập dữ liệu so với giá trị trung bình đã tính ra. Căn bậc hai của phương sai là độ lệch chuẩn (σ).
Độ lệch chuẩn của dấu hiệu x, ký hiệu: Sx
Nếu độ lệch chuẩn bằng 0, suy ra phương sai bằng 0, suy ra các giá trị quan sát cũng chính là giá trị trung bình. Nói cách khác là không có sự biến thiên.
Nếu độ lệch chuẩn càng lớn, suy ra sự biến thiên xung quanh giá trị trung bình càng lớn.
Công thức tính phương sai
Phương sai được tính bằng cách xác định giá trị chênh lệch giữa mỗi số trong tập dữ liệu với giá trị trung bình, sau đó bình phương các chênh lệch nhằm cho chúng mang giá trị dương và không triệt tiêu lẫn nhau. Cuối cùng chia tổng số lượng quan sát trong tập dữ liệu.
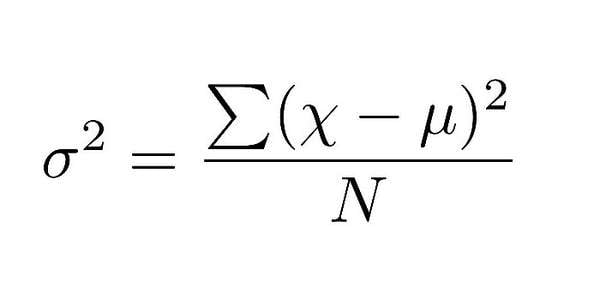 margin:0px;" title="Tìm hiểu về phương sai, công thức tính phương sai đúng nhất"> margin:0px;" title="Tìm hiểu về phương sai, công thức tính phương sai đúng nhất"> |
| Công thức tính phương sai |
Trong đó:
xi là giá trị của quan sát thứ i
µ là giá trị trung bình của tập dữ liệu
n là số quan sát trong tập dữ liệu
Phương sai là một trong những thông số quan trọng để các nhà đầu tư xem xét phân bổ tài sản cùng với hệ số tương quan. Việc xác định phương sai của lợi nhuận tài sản giúp các nhà đầu tư phát triển danh mục đầu tư tốt hơn bằng cách tối ưu hóa sự đánh đổi giữa rủi ro và lợi nhuận với mỗi khoản đầu tư của họ.
Căn bậc hai của phương sai là độ lệch chuẩn (σ).
Ví dụ về phương sai
Để hiểu rõ hơn về khái niệm phương sai, bạn có thể xem qua ví dụ cụ thể về đầu tư dưới đây:
Lợi tức của một cổ phiếu là:
Trong năm đầu tiên:10%.
Trong năm hai: 20%.
Trong năm ba: -15%.
Trung bình lợi nhuận của ba năm này là 5%. Sự khác biệt giữa mỗi lần hoàn vốn và giá trị trung bình là 5%, 15% và -20% cho mỗi năm liên tiếp.
Bình phương tương ứng của các độ lệch này sẽ là: 25%, 225% và 400%.
Tổng các độ lệch bình phương này là 650%.
Ta chia tổng số 650% cho số lần hoàn vốn (3 trong các trường hợp này) sẽ có được phương sai là 216,67%. Lấy căn bậc hai của phương sai sẽ ra độ lệch chuẩn là 14,72% cho lợi nhuận.
Cách sử dụng phương sai và độ lệch chuẩn
Phương sai đo lường sự khác biệt đến điểm trung vị hoặc trung bình. Đối với các nhà đầu tư, sự biến động là thước đo rủi ro. Do đó, xác định phương sai có thể giúp nhà đầu tư xác định rủi ro mà họ phải chịu khi mua một chứng khoán cụ thể.
Một phương sai lớn cho biết các số trong tập dữ liệu nằm cách xa giá trị trung bình và biến động lớn, trong khi phương sai nhỏ chỉ ra điều ngược lại.
Giá trị phương sai bằng 0 chỉ ra rằng tất cả các giá trị trong một tập dữ liệu là giống hệt nhau. Hay không có sai số. Tất cả các phương sai không bằng 0 sẽ là số dương.
Độ lệch chuẩn có ứng dụng khá hay đó là giúp chuẩn hóa giá trị của hai dãy số khác nhau về cùng một miền dữ liệu.
Ưu điểm và nhược điểm của phương sai
Các nhà thống kê sử dụng phương sai để xem các số riêng lẻ có quan hệ với nhau như thế nào trong một tập dữ liệu.
Ưu điểm của phương sai là nó xem tất cả các sai lệch so với giá trị trung bình giống nhau bất kể hướng của chúng, vì vậy chúng không bị triệt tiêu. Thực tế phương sai không thể nào bằng 0 do không thể không có sự sai số nào trong một tập dữ liệu.
Nhược điểm của phương sai là nó tăng trọng số cho các dữ liệu ngoại lai, những dữ liệu ngoại lai có giá trị khác xa so với giá trị trung bình. Khi bình phương những giá trị này có thể sẽ làm lệch tập dữ liệu.
Hạn chế của phương sai là nó không dễ để diễn giải. Người dùng phương sai thường sử dụng nó chủ yếu để lấy căn bậc hai của nó, hay độ lệch chuẩn của tập dữ liệu.
Phương sai trong đầu tư
Phương sai là một tham số quan trọng trong phân bổ tài sản đầu tư, được sử dụng cùng với hệ số tương quan, xác định phương sai của tài sản có thể giúp nhà đầu tư phát triển danh mục đầu tư nhằm tối ưu hóa sự đánh đổi giữa rủi ro và lợi nhuận.
Tuy nhiên, rủi ro hoặc biến động thường được thể hiện dưới dạng độ lệch chuẩn thay vì phương sai bởi vì nó dễ hiểu hơn.
Minh Đức

